Content for TR 22.804 Word version: 16.3.0
4.3.3 Dependable communication
4.3.3.1 Introduction
4.3.3.2 System dependability
4.3.3.3 Definition of communication dependability and its implications
...
...
4.3.3 Dependable communication p. 30
4.3.3.1 Introduction p. 30
According to ISO, dependability (of an item) is the "ability to perform as and when required" [20]. This is a paramount property of any automation system. Automation systems that are not dependable can, for instance, be unsafe or they can exhibit low productivity. Clause 4.3.3.2 discusses system dependability in further detail, and this information is used to analyse communication dependability and its implication for 5G systems in Clause 4.3.3.3.
4.3.3.2 System dependability p. 30
Dependability can be broken down into five system properties: reliability, availability, maintainability, safety, and integrity (see Figure 4.3.3.2-1) [44].
![Copy of original 3GPP image for 3GPP TS 22.804, Fig. 4.3.3.2-1: The five facets of system dependability: reliability, availability, maintainability, safety, and integrity [44]](../img/tinv-22-804-4.3.3.2-1.gif)
Figure 4.3.3.2-1: The five facets of system dependability: reliability, availability, maintainability, safety, and integrity [44]
(⇒ copy of original 3GPP image)
(⇒ copy of original 3GPP image)
Definitions for each system property are provided in Table 4.3.3.2-1.
| System property | Definition |
|---|---|
| Reliability | Continuity of correct operation |
| Availability | Readiness for correct operation |
| Maintainability | Ability to undergo modifications and repairs |
| Safety | Absence of catastrophic consequences on user(s) and environment |
| Integrity | Absence of improper system alterations |
Availability indicates whether the system is ready for use at a given time. This system property is typically quantified by the percentage of time during which a system operates correctly. Reliability indicates how long correct operation continues. This system property is typically defined as the (mean) time between failures. Both properties are illustrated with and example. In this example the system has an availability of 99,99%. This implies that its unavailability is 0,01%, or 53 min on average per year. If the system fails on average thrice a year then, reliability, quantified as the mean time between failures, is four months.
Availability and reliability are closely related to the productivity of a system. A system featuring a low availability is rarely ready for operation and is thus characterised by low productivity. If the system reliability is low, i.e. the time between failures is short, the system comes often to a halt, which contravenes continuous productivity.
4.3.3.3 Definition of communication dependability and its implications p. 31
4.3.3.3.1 Introduction p. 31
A composite system, where every subsystem is instrumental to the operation of the composite system, is not dependable if any of the subsystems is undependable. This has the following implications for the use of communication systems in general, and 5G systems in particular. Figure 4.3.3.3.1-1 depicts a generic, distributed automation system, where the automation functions interact via a communication system.
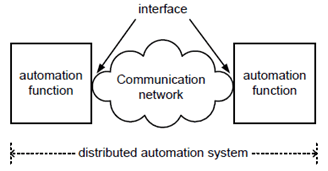
Figure 4.3.3.3.1-1: Example of a distributed automation system consisting of automation functions and a communication network
(⇒ copy of original 3GPP image)
(⇒ copy of original 3GPP image)
In this example, all three subsystems, i.e. the automation functions and the communication network need to be dependable for the automation system to be dependable.
Communication dependability is the property of a dependable communication system. According to IEC 61907, network dependability is the "ability to perform as and when required to meet specified communication and operational requirements" [2]. This definition largely agrees with 3GPP's own definition: "A performance criterion that describes the degree of certainty (or surety) with which a function is performed regardless of speed or accuracy, but within a given observational interval" [1]. What does communication dependability imply in praxis from the vantage point of the automation functions? We address this for each of the five system properties in Figure 4.3.3.2-1.
4.3.3.3.2 Reliability p. 31
According to IEC 61907, network reliability is the "ability to perform as required for a given time interval, under given conditions" [2].
Automation functions need highly reliable communication. As a rule of thumb the more infrequent communication is unavailable the better.
Note that reliability in the context of dependability has a different meaning than employed in TS 22.261 [], which defines it as the "percentage value of the amount of sent network layer packets successfully delivered to a given node within the time constraint required by the targeted service, divided by the total number of sent network layer packets" [3]. This definition is more akin to the definition of network availability (see Clause 4.3.3.3.3) and it focuses on the inner working of the network rather than the end-to-end experience of functions consuming the network's communication capabilities. In order to avoid confusion, reliability of a communication system is henceforth referred to as communication service reliability. We discuss this in more detail in Clause 4.3.4.
4.3.3.3.3 Availability p. 32
According to IEC 61907, network availability is the "ability to be in a state to perform as and when required, under given conditions, assuming that the necessary external resources are provided" [2]. Note that given conditions "would include aspects that affect reliability, maintainability and maintenance support performance" [2]. It is important to point out that a communication network that does not meet the communication requirements of the automation functions, e.g. a maximum end-to-end latency, are considered to be unavailable.
4.3.3.3.4 Maintainability p. 32
According to IEC 61907, network maintainability is the "ability to be retained in, or restored to, a state in which it can perform as required under given conditions of use and maintenance" [2]. Note that given conditions of maintenance "include the procedures and resources to be used" [2]. "Maintainability may be quantified using such measures as, mean time to restoration, or the probability of restoration within a specified period of time" [2]. Clause 4.3.4 discusses what maintainability implies for a dependable communication service.
4.3.3.3.5 Safety p. 32
As introduced in Clause 4.3.3.2, safety stands for the absence of catastrophic consequences on user(s) and environment. For a distributed automation system this implies that neither the automation functions including their physical embodiment, nor the processes, nor the environment should be damaged by the communication system. This communication system property is-for instance-addressed through regulations such as directive 2014/53/EU [21]. Note that in most automation implementations the safety of the communication systems can be treated separately and that the overall safety of the distributed automation system is addressed by automation functions such as functional-safety mechanisms.
4.3.3.3.6 Integrity p. 32
According to IEC 61907, network integrity is the "ability to ensure that the data throughput contents are not contaminated, corrupted, lost or altered between transmission and reception" [2]. Note that this communication system property is-in the communication network community-seen as an atomic property of information security in communication systems. More on this in Clause 6.1.
4.3.3.3.7 Implications for 5G systems p. 32
In order to be suitable for automation in vertical domains, 5G systems need to be dependable, i.e. they need to come with the system properties in Clause 4.3.3.3.2 to Clause 4.3.3.3.6. What particular requirements each property needs to meet depends on the particularities of the domain and the use case. More on this in Clause 5. Clause 4.3.4 addresses what the request for communication dependability implies for communication services provided by 5G systems.
It is important to understand that the relationship between communication service availability, communication service continuity, communication service reliability, and the probability of an erroneous message transmission anything but trivial. Understanding this relationship is also important since communication service in this document is not defined according to TL 9000 [56], for example.
According to ISO/IEC [54], service continuity is "capability to manage risks and events that could have serious impact on a service or services in order to continually deliver services at agreed levels". According to TS 22.261, the service continuity is "the uninterrupted user experience of a service that is using an active communication when a UE undergoes an access change without, as far as possible, the user noticing the change". The concept of service continuity in TS 22.261 is very narrow and limited to a "capability" of confronting only an event of "UE undergoing an access change". The communication service continuity can be impacted by many other events either in the control plane or the user plane, or both, such as intervening exceptions or anomalies, whether scheduled or unscheduled, malicious, intentional or unintentional [55]. For a reliable system, any event which might impact to the communication service continuity is needed to be considered.
A maximum tolerable communication service unavailability of, for instance, 10-6 does not always imply a maximum tolerable probability of erroneous and prohibitively delayed end-to-end message transmission of 10-6 .One of the main reasons for why this generally is not the case is a non-zero survival time. This is illustrated with the example below.
Survival time revisited
According to TS 22.261, the survival time is "the time that an application consuming a communication service may continue without an anticipated message" [3]. Anticipation implies following aspects: timeliness and correctness. The communication service continuity implies the following three conditions: firstly, the message needs to arrive in time (timeliness); secondly, only uncorrupted messages are accepted by the receiver; and thirdly, the received messages need to be processed and sent out from 3GPP 5G system to the target automation function. So, if at least one of these conditions is not fulfilled, a timer is started by the automation function. Upon expiration of the timer, the communication service for that application is declared "unavailable" (service discontinuity; also see Clause A.2). The expiration time is referred to as the survival time.
Influence of survival time on the acceptable probability of untimely message transmission
To simplify the discussion, it is assumed that none of the transmitted messages is corrupted or lost because of an anomaly in the communication system and that thus the only cause of unavailability of a communication service is that the end-to-end latency of a message lies outside the interval specified by the jitter (see Clause A.3 for more details on jitter and timeliness).
Example: the update time is 50 ms. A survival time of 0 ms implies that any untimely arrival of a message (e.g. the update time of that message delivery is outside of the interval specified by the jitter) triggers the communication to be declared as "down" by the automation function. Thus, if the aggregate communication service unavailability is specified as 10-6 and lower, an untimely arrival of messages shall only occur up to 1 in one million cycles for periodic communication.
The situation changes markedly for non-zero survival times. For a survival time of, e.g., 100 ms (see table 7.2.2-1 in [3]), the target automation function waits two more cycles after a delayed message before it declares the communication service as unavailable. If the likelihood of a single untimely arrival is p, and if the sequential untimely arrivals are independent of each other, the likelihood of three untimely arrivals in a row is p3, which is the likelihood for the communication service to be unavailable. For a target unavailability of 10-6, the acceptable likelihood of a single untimely arrival can thus be as high as 0,01.
The implications for the likelihood of a single untimely arrival are even more relaxed for longer survival times. For automated commuter-train control, the survival time is up to five times longer than the cycle time (see Clause 5.1.1.2). Thus, in this case, six untimely arrivals have to occur in a row before the communication service is declared unavailable. The likelihood of such an event is p6, which, for a target unavailability of 10-6 for this commuter-train control, implies that p ≤ 0,1. In other words 1 out of 10 messages (!) may arrive outside the time interval specified by the receiver while keeping the automation function consuming this communication service operational.
Influence of communication service reliability on the probability of erroneous message transmission
The above examples are simplistic since the influence of communication service reliability has not been taken into account. This influence is also discussed for a concrete example. In this example, it is assumed that the user of the aforementioned communication service expects the downtime of the system to be contingent and to only occur once a year. An unavailability of 10-6 translates thus into a maximum continuous unavailability of ~ 30 s per year. The implication for the tolerable erroneous transmission probability is not trivial, since many scenarios can result in such an excellent performance. One possible extreme is that no erroneous transmission occurs during the most of the year, but then the communication times out for 30 s in a row. Another possible extreme is that the every cycle is erroneous, but that a correct message is delivered before the survival timer runs out. In such a case, the communication service unavailability is actually zero. In praxis, a comprehensive stochastic analysis is needed in order to understand the implications of communication service reliability on the tolerable probability of erroneous message transmission, and a range of measurements may need to be defined and carried out in order to infer comprehensive performance requirements that guarantee high communication fidelity. An example for such a performance requirement is related to the maximum service unavailability time.
Implications of data packet fragmentation for reliability
According to TS 22.261, reliability is defined as percentage value of the amount of sent network layer packets successfully delivered to a given node within the time constraint required by the targeted service, divided by the total number of sent network layer packets [3]. If the messages to be transported by the communication service are so short that they are not broken into several packets, then the above discussion can also be applied to reliability. However, in case messages are broken into several packets then the implications of a communication service unavailability for the reliability of a 5G system is contingent on implementation details such as how messages are constructed from packets and whether timeliness issues in one packet influence that of an adjacent packet.