Content for TS 23.032 Word version: 18.1.0
6 Coding
6.1 Point
6.1a High Accuracy Point
6.2 Uncertainty
6.2a High Accuracy Uncertainty
6.2b High Accuracy Extended Uncertainty
6.3 Altitude
6.3a High Accuracy Altitude
6.4 Uncertainty Altitude
6.5 Confidence
6.6 Radius
6.7 Angle
...
...
6 Coding p. 15
6.1 Point p. 15
The co-ordinates of an ellipsoid point are coded with an uncertainty of less than 3 metres.
The latitude is coded with 24 bits: 1 bit of sign and a number between 0 and 223-1 coded in binary on 23 bits. The relation between the coded number N and the range of (absolute) latitudes X it encodes is the following (X in degrees):
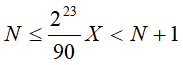
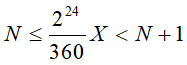
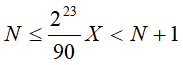
except for N=223-1, for which the range is extended to include N+1.
The longitude, expressed in the range -180°, +180°, is coded as a number between -223 and 223-1, coded in 2's complement binary on 24 bits. The relation between the coded number N and the range of longitude X it encodes is the following (X in degrees):
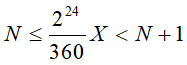
6.1a High Accuracy Point p. 15
The co-ordinates of a high accuracy ellipsoid point are coded with a resolution of less than 5 millimetre for latitude, and less than 10 millimetre for longitude.
The latitude for a high accuracy point, expressed in the range -90°, +90°, is coded as a number between -231 and 231-1, coded in 2's complement binary on 32 bits. The relation between the latitude X in the range [-90°, 90°] and the coded number N is:

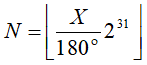

where 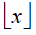 denotes the greatest integer less than or equal to x (floor operator).
denotes the greatest integer less than or equal to x (floor operator).
The longitude for a high accuracy point, expressed in the range -180°, +180°, is coded as a number between -231 and 231-1, coded in 2's complement binary on 32 bits. The relation between the longitude X in the range [-180°, 180°) and the coded number N is:
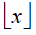 denotes the greatest integer less than or equal to x (floor operator).
denotes the greatest integer less than or equal to x (floor operator).
6.2 Uncertainty p. 16
A method of describing the uncertainty for latitude and longitude has been sought which is both flexible (can cover wide differences in range) and efficient. The proposed solution makes use of a variation on the Binomial expansion. The uncertainty r, expressed in metres, is mapped to a number K, with the following formula:
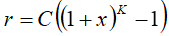 with C = 10 and x = 0,1. With 0 ≤ K ≤ 127, a suitably useful range between 0 and 1800 kilometres is achieved for the uncertainty, while still being able to code down to values as small as 1 metre. The uncertainty can then be coded on 7 bits, as the binary encoding of K.
with C = 10 and x = 0,1. With 0 ≤ K ≤ 127, a suitably useful range between 0 and 1800 kilometres is achieved for the uncertainty, while still being able to code down to values as small as 1 metre. The uncertainty can then be coded on 7 bits, as the binary encoding of K.
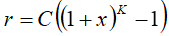
| Value of K | Value of uncertainty |
|---|---|
| 0 | 0 m |
| 1 | 1 m |
| 2 | 2,1 m |
| - | - |
| 20 | 57,3 m |
| - | - |
| 40 | 443 m |
| - | - |
| 60 | 3 km |
| - | - |
| 80 | 20 km |
| - | - |
| 100 | 138 km |
| - | - |
| 120 | 927 km |
| - | - |
| 127 | 1800 km |
6.2a High Accuracy Uncertainty p. 16
The high accuracy uncertainty r, expressed in metres, is mapped to a number K, with the following formula:
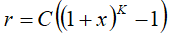 with C = 0.3 and x = 0.02. With 0 ≤ K ≤ 255, a suitably useful range between 0 and 46.49129 metres is achieved for the high accuracy uncertainty, while still being able to code down to values as small as 6 millimetre. The uncertainty can then be coded on 8 bits, as the binary encoding of K.
with C = 0.3 and x = 0.02. With 0 ≤ K ≤ 255, a suitably useful range between 0 and 46.49129 metres is achieved for the high accuracy uncertainty, while still being able to code down to values as small as 6 millimetre. The uncertainty can then be coded on 8 bits, as the binary encoding of K.
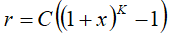
| Value of K | Value of uncertainty |
|---|---|
| 0 | 0 m |
| 1 | 0.006 m |
| 2 | 0.01212 m |
| - | - |
| 20 | 0.14578 m |
| - | - |
| 40 | 0.36241 m |
| - | - |
| 60 | 0.68430 m |
| - | - |
| 80 | 1.16263 m |
| - | - |
| 100 | 1.87339 m |
| - | - |
| 120 | 2.92954 m |
| - | - |
| 127 | 3.40973 m |
| - | - |
| 255 | 46.49129 m |
6.2b High Accuracy Extended Uncertainty p. 17
The high accuracy extended uncertainty r, expressed in metres, is mapped to a number K, with the following formula:
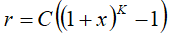 with C = 0.3 and x = 0.02594, with 0 * K * 253, and r = 200 m with K=254, and r > 200 m with K=255 a suitably useful range between 0 and 200 metres is achieved for the high accuracy uncertainty, while still being able to code down to values as small as 8 millimetres. The uncertainty can then be coded on 8 bits, as the binary encoding of K.
with C = 0.3 and x = 0.02594, with 0 * K * 253, and r = 200 m with K=254, and r > 200 m with K=255 a suitably useful range between 0 and 200 metres is achieved for the high accuracy uncertainty, while still being able to code down to values as small as 8 millimetres. The uncertainty can then be coded on 8 bits, as the binary encoding of K.
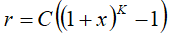
| Value of K | Value of uncertainty |
|---|---|
| 0 | 0 m |
| 1 | 0.00778 m |
| 2 | 0.01577 m |
| - | - |
| 20 | 0.20068 m |
| - | - |
| 40 | 0.53560 m |
| - | - |
| 60 | 1.09457 m |
| - | - |
| 80 | 2.02744 m |
| - | - |
| 100 | 3.58434 m |
| - | - |
| 120 | 6.18271 m |
| - | - |
| 127 | 7.45551 m |
| - | - |
| 253 | 195.12396 m |
| 254 | 200 m |
| 255 | > 200 m |
6.3 Altitude p. 18
Altitude is encoded in increments of 1 meter using a 15 bit binary coded number N. The relation between the number N and the range of altitudes a (in metres) it encodes is described by the following equation:
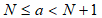 Except for N=215-1 for which the range is extended to include all greater values of a.
The direction of altitude is encoded by a single bit with bit value 0 representing height above the WGS84 ellipsoid surface and bit value 1 representing depth below the WGS84 ellipsoid surface.
Except for N=215-1 for which the range is extended to include all greater values of a.
The direction of altitude is encoded by a single bit with bit value 0 representing height above the WGS84 ellipsoid surface and bit value 1 representing depth below the WGS84 ellipsoid surface.
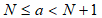 Except for N=215-1 for which the range is extended to include all greater values of a.
Except for N=215-1 for which the range is extended to include all greater values of a.
6.3a High Accuracy Altitude p. 18
High accuracy altitude is encoded as a number N between -64000 and 1280000 using 2's complement binary on 22 bits. The relation between the number N and the altitude a (in metres) it encodes is described by the following equation:
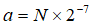 So, the altitude for a high accuracy point, with a scale factor of 2-7, ranges between -500 metres and 10000 metres. The altitude is encoded representing height above (plus) or below (minus) the WGS84 ellipsoid surface.
So, the altitude for a high accuracy point, with a scale factor of 2-7, ranges between -500 metres and 10000 metres. The altitude is encoded representing height above (plus) or below (minus) the WGS84 ellipsoid surface.
6.4 Uncertainty Altitude p. 18
The uncertainty in altitude, h, expressed in metres is mapped from the binary number K, with the following formula:
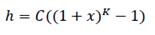 with C = 45 and x = 0,025. With 0 ≤ K ≤ 127, a suitably useful range between 0 and 990 meters is achieved for the uncertainty altitude. The uncertainty can then be coded on 7 bits, as the binary encoding of K.
with C = 45 and x = 0,025. With 0 ≤ K ≤ 127, a suitably useful range between 0 and 990 meters is achieved for the uncertainty altitude. The uncertainty can then be coded on 7 bits, as the binary encoding of K.
| Value of K | Value of uncertainty altitude |
|---|---|
| 0 | 0 m |
| 1 | 1,13 m |
| 2 | 2,28 m |
| - | - |
| 20 | 28,7 m |
| - | - |
| 40 | 75,8 m |
| - | - |
| 60 | 153,0 m |
| - | - |
| 80 | 279,4 m |
| - | - |
| 100 | 486,6 m |
| - | - |
| 120 | 826,1 m |
| - | - |
| 127 | 990,5 m |
6.5 Confidence p. 18
The confidence by which the position of a target entity is known to be within the shape description, (expressed as a percentage) is directly mapped from the 7 bit binary number K, except for K=0 which is used to indicate 'no information', and 100 < K ≤128 which should not be used but may be interpreted as "no information" if received.
6.6 Radius p. 19
Inner radius is encoded in increments of 5 meters using a 16 bit binary coded number N. The relation between the number N and the range of radius r (in metres) it encodes is described by the following equation:
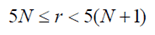 Except for N=216-1 for which the range is extended to include all greater values of r. This provides a true maximum radius of 327,675 meters.
The uncertainty radius is encoded as for the uncertainty latitude and longitude.
Except for N=216-1 for which the range is extended to include all greater values of r. This provides a true maximum radius of 327,675 meters.
The uncertainty radius is encoded as for the uncertainty latitude and longitude.
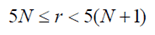 Except for N=216-1 for which the range is extended to include all greater values of r. This provides a true maximum radius of 327,675 meters.
Except for N=216-1 for which the range is extended to include all greater values of r. This provides a true maximum radius of 327,675 meters.
6.7 Angle p. 19
Offset and Included angle are encoded in increments of 2° using an 8 bit binary coded number N in the range 0 to 179. The relation between the number N and the range offset (ao) and included (ai) of angles (in degrees) it encodes is described by the following equations:
Offset angle (ao)
2 N <= ao < 2 (N+1) Accepted values for ao are within the range from 0 to 359,9...9 degrees.
Included angle (ai)
2 N < ai <= 2 (N+1) Accepted values for ai are within the range from 0,0...1 to 360 degrees.